5BLDのXセンターでより良い分析優先順位を探索する試み
はじめに
こんにちは、酢酸ことSakakiです。
この記事はSpeedcubing Advent Calendar 2023の1日目の記事です。
昨日の記事 : 初日なので無し
明日の記事 : 『もちろんメガミンクス(ついでに僕の誕生日です)』 (佐村健人さん)
この記事では、5BLDのXセンターを分析する際に、どのような順番で辿るのがよいかについて説明します。
課題感、ゴール
多分割BLDのセンター分析は、エッジやコーナーよりも自由度が高いです。エッジやコーナーは1通りの道筋を進んでいき、ループが切れた時だけどこから再開するのかを自由に決めますが、多分割BLDの場合は、例えばバッファにF面のステッカーが入っていた場合、それをF面の空いているステッカー4つのどこに移してもよいです。
では、どのような分析をするとよいのでしょうか? これが本記事のテーマです。直観的には、6つの面全てで規則的に時計回りや反時計回りで統一すると、3-styleでのインターチェンジの関係のステッカーが分析に現れやすくなり、セットアップの手数が減るように思えます。これを検証していきましょう。
設定
4BLDにすると開始面を自由に選べてしまうという難しさがあるので、5BLDで考えます。
バッファはUblとし、3-style手順は私の手順*1で検証します。
違う手順だったらどうかや違うバッファだったらどうかなど、チューニングできるポイントは無数にあると思いますが、キリが無いので本記事ではバッファと手順は固定のものとして考えます。
検証に使ったコードは公開するので、興味がある人は自分のバッファや手順で動かしてください。
なお、分析はU面回避する戦略にしていないので1手順ぶん余分に計上されている可能性があります。
U面をどのように回避するかまではロジックとして組み込めなかったことと、そこまで考慮するとパターン数が膨大になるためです。
また、ループの開始面はR,F,L,B,D,Uの優先順位で固定し、6!=24通りの探索はしていません。
手数の数え方
- 外層の回転についてはQuarter Turn Metric (QTM) を用います。つまり、90度回転で1手とします
- FMC的な手数ではなく、実際に回す時の時間の長さを気にしています
- スライスムーブについては、u, u'は1手、それ以外のスライスムーブは2手とします
- 持ち替えは3手とします。ただし、
x yのように一連の持ち替えについてはまとめて3手とカウントします
分析優先順位のパターン
規則的な場合
1つの面について、
- 開始ステッカーをどれにするか: 4通り (U面の場合はバッファを除いて3通り)
- 時計回り/反時計回りのどちらで巡るか: 2通り
これが6面ぶんあるので、
(4 * 2) ^ 5 * (3 * 2) = 196,608通り
ランダムな場合
1つの面の中での優先順位が4!=24通り (U面は3!=6通り)
(4!)5 * 3! = 47,775,744通り
現実的な時間で扱えるように、ランダムにサンプリングします。
計測手法
スクランブルというものは、ステッカー24枚をシャッフルしたものとします。
まず、スクランブルを400個*2サンプリングして固定します。スクランブル1からスクランブル400まで番号を振っておきます。
次に、ランダムな分析優先順位について400個*3サンプリングして固定します。分析優先順位は「ランダム分析優先順位1」から「ランダム分析優先順位400」まで番号を振っておきます。
ランダムな優先順位400個 + 196,608通りの規則的な優先順位に対し、400個のスクランブルに対しての分析結果を見ます。
スクランブルごとに優先順位に従って分析し、それを3-style手順に置き換えて手数を算出します。
400個のスクランブルでの手数の平均、中央値、不偏標準偏差を計算します。
ランダムな分析優先順位については、「400個のスクランブルに対する平均手数」のマクロ平均を算出します。
結果と考察
| 分析優先順位 | 平均 | 中央値 | 不偏標準偏差 |
|---|---|---|---|
| 規則的 最悪 (No.42894) | 179.2 | 178 | 19.90 |
| ランダム平均 | 174.3 | - | - |
| 規則的 時計 (No.21825) | 171.8 | 172 | 17.72 |
| 規則的 最良 (No.78039)*4 | 169.9 | 172 | 18.07 |


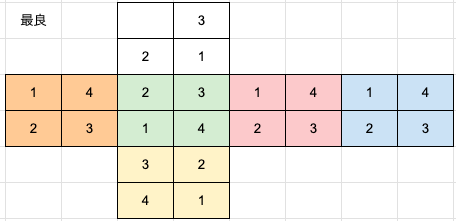
- 規則的であっても、ランダムに劣る場合がある
- 規則的(時計)はシンプルで覚えやすい上に、そんなに悪くない
- 規則的(最良)は、L面・R面・B面は同じ順番なのでインターチェンジしやすい
- 規則的(最良)のF面・D面は少しズレている。F面←→バッファ、D面←→バッファへのインターチェンジが重視されているかもしれない
- とはいえ、規則的(時計回り)と規則的(最良)で2手しか違わないので、こだわるポイントではないかもしれない
違いが小さすぎる上に、どこがどう効いているのかを見極めるのが難しいので、うまく考察できていないです。
許容誤差5%としていますが、170手の5%は8.5手で大きすぎるので、本来は10000サンプルで計算すべきかもしれません。しかし、計算時間的に厳しいです。
今後の課題
これまでに説明していたが、今回の実験では多くの条件を制限しています。
- スクランブル数は400、許容誤差は5%と大きい
- バッファ
- 手順
- U面回避: しない
- ループの開始面
計算時間をかけてこれらの条件を変えて探索すれば、さらに良い結果が得られる可能性があります。
また、今回の実験では、客観性を重視して手数を指標としましたが、もし3-styleを回すのにかかる秒数を客観的に導入できれば、タイムという実用的な指標での議論ができます。 1人(私)のタイムでは私の3-style手順の得意・不得意のバイアスが大きいですが、複数の競技者のタイムを得て平均することで偏りを減らせば、タイムを基準に議論することができる可能性があります。
+センターでも同様のシミュレートができます。原理的にはXセンターとほぼ変わらないので、単純な時計回りで充分という結果になりそうです。
本記事を書くために作成したスクリプトは以下のページで公開しています。
https://github.com/sakabar/speedcubing-advent-calendar-2023-script